GES: Generalized Exponential Splatting for Efficient Radiance Field Rendering
[CVPR 2024]

Abstract
Advancements in 3D Gaussian Splatting (GS) have significantly accelerated 3D reconstruction and generation. However, it may require a very large number of Gaussians, which can become a substantial memory footprint. This paper introduces GES (Generalized Exponential Splatting), a novel representation that employs Generalized Exponential Function (GEF) to model 3D scenes, requiring far fewer particles to represent a scene and thus significantly outperforming Gaussian Splatting methods in efficiency with a plug-and-play replacement ability for Gaussian-based utilities. GES is validated theoretically and empirically in both principled 1D setup and realistic 3D contexts. It is shown to more accurately represent signals with sharp edges, which are typically challenging for Gaussians due to their inherent low-pass characteristics of the Gaussian function.Our empirical analysis demonstrates that GEF outperforms Gaussians in fitting natural-occurring signals (e.g. squares, triangles, parabolic signals), thereby reducing the need for extensive splitting operations that increase the memory footprint of Gaussian Splatting. With the aid of a frequency-modulated loss, GES achieves competitive performance in novel-view synthesis standard benchmarks while requiring less than half the memory storage of Gaussian Splatting and increasing the rendering speed by up to 39%.
Video
GEF Overcomes Gaussian's Low-Pass Limitation
Gaussian is limited by its low-pass property. See the figure below for the fact that high-frequency signals are filtered out by Gaussian. Thus many Gaussian components are required in the sharp edges in order to fit the high-frequency signals.

We propose a drop-in replacement of Gaussian: Generalized Exponential Function (GEF), which is defined as \[f_{\beta}(x) = Ae^{-\left(\frac{|x - \mu|}{\alpha}\right)^\beta}\]
GEF covers a family of functions as shown below, and reduces to the Gaussian function followed in 3D gaussian splatting when \[\alpha=1, \mu=0, \beta = 2\].
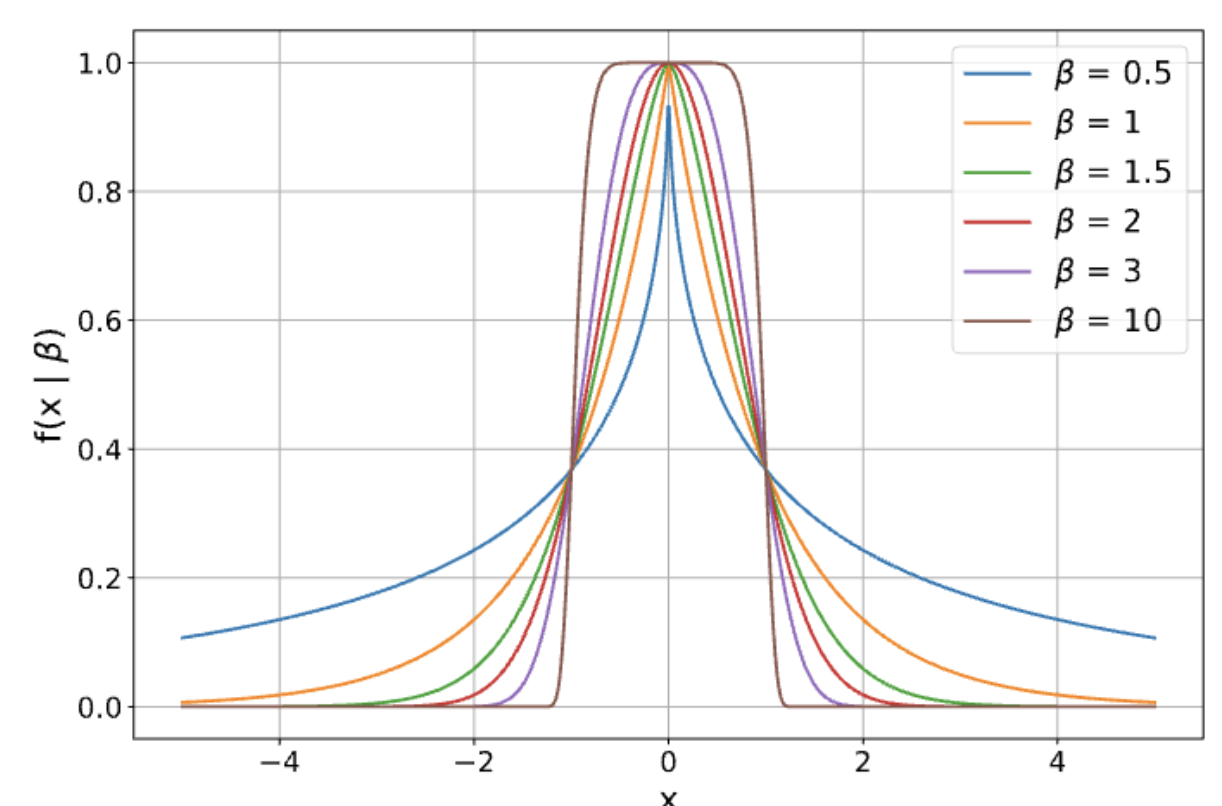
GEF Fits Signals with Fewer Components than Gaussian
Gaussian
Generalized Exponential Function (GEF)
GEF fits signals with much fewer components. Thus, theoretically, GEF can reconstruct the same signals with less storage than Gaussian.
GES Can Be Used as A Drop-In Replacement of Gaussian Splatting to Reduce Size


Main Results

Detailed Numerical Results (per Scene)
Citation
@InProceedings{hamdi_2024_CVPR,
title = {GES: Generalized Exponential Splatting for Efficient Radiance Field Rendering},
author = {Hamdi, Abdullah and Melas-Kyriazi, Luke and Mai, Jinjie and Qian, Guocheng and Liu, Ruoshi and Vondrick, Carl and Ghanem, Bernard and Vedaldi, Andrea},
booktitle = {Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)},
month = {June},
year = {2024},
pages = {19812-19822},
}


